Jaglo
Społeczność Astropolis-
Postów
31 -
Dołączył
-
Ostatnia wizyta
Ostatnie wizyty
Blok z ostatnimi odwiedzającymi dany profil jest wyłączony i nie jest wyświetlany użytkownikom.
Osiągnięcia Jaglo
12
Reputacja
-
Przepraszam osoby zainteresowane tematem i chcące merytorycznie dyskutować. Musimy się liczyć z różnego rodzaju komentarzami, które wyrażają światopogląd innych forumowiczów. Pojawiają się próby wywierania presji na to, jakimi zagadnieniami się zajmujemy i wmawiające nam, że nie należy w tym wątku pisać. Jak to potraktować? Podpowiem: nie powinno się słuchać doradców, których wpisy są niemerytoryczne i poza tematem. Wpisów off-top najlepiej w ogóle nie czytać. A jeżeli już przeczytamy, to nie można ulegać sugestiom takich osób. Nie dajmy się im zmanipulować, zawstydzić czy zastraszyć. O zabraniu głosu niech każdy decyduje sam za siebie. Nie można pozwolić, by ciekawe i ważne tematy były sabotowane
-
To, co postuluję w modelu, zapisane jest w 5 wpisach: - 4 maja 2019 - 14 lipca 2019 (tylko pierwsza cześć, bo z rozważań o energii potencjalnej się wycofałem) - 18 listopada 2019 - 12 czerwca 2020 (wycofałem się z tego) - 7 kwietnia 2021 - 26 kwietnia 2021 Mogę udostępnić wersję w doc, w której są czytelne wzory, uwzględniającą te wpisy i uwagi, które padały. W skrócie: 1. Model kosmosu Kosmos jest 4-wymiarowy, tzn. jest przestrzenią R 4. Wielki wybuch wywołał ruch w czwartym wymiarze, dlatego nie zauważamy tego wymiaru w taki sposób jak 3 pozostałe. Żyjemy na powierzchni 4-wymiarowej rozmaitości zwanej glomem (ang. glome). Ta powierzchnia to przestrzeń 3-wymiarowa. Wynika stąd, że przestrzeń kosmosu jest zamknięta. Gdyby zatrzymać ekspansję, można by oblecieć wszechświat dookoła, udając się w dowolnym kierunku, analogicznie jak można opłynąć i objechać nasz ziemski glob, wybierając dowolny kierunek. Zamknięcie przestrzeni 3-wymiarowej daje logiczne wytłumaczenie dla pytań o wielkość kosmosu, jego skończoność/nieskończoność i granice. Wyjaśnia też obserwacje astronomiczne tzw. mocnej zasady kosmologicznej. 2. Prawo Hubble'a Prawo Hubble'a jest prostą konsekwencją ruchu w 4. wymiarze. Im większa odległość kątowa między obiektami, tym proporcjonalnie większy przyrost przestrzeni między nimi. Wyjaśnienie prawdziwe dla statycznej powierzchni glomu, jest również prawdziwe w warunkach jednostajnej ekspansji. 3. Odległość Odległość w 3D między obiektami rośnie w czasie: d(T+t) = d(T) * (1 + t/T) Dotyczy to nie tylko galaktyk, ale dowolnych obiektów (np. odległość Ziemia - Księżyc, czy między gwiazdami). Nie wymaga to udziału żadnej energii. 4. Czas Odległość w 4D mierzy się wzorem: D2 = x2 + y2 + z2 + (ct)2 więc dla ciała w spoczynku w 3D mamy szczególny przypadek: D = ct Widać więc, że czas i odległość to pojęcia blisko ze sobą związane. Według tej teorii nasze intuicje odnośnie do czasu powinny być zrewidowane. Np. pojęcie teraźniejszości czy równoczesności. Np. od Słońca dzieli nas 8 minut. Możemy wysłać w jego pobliże sondę z zegarem zsynchronizowanym z ziemskim czasem. Naturalnie będziemy myśleć, że na sondzie obowiązuje ten sam czas, co na Ziemi - uzyskujemy niby tę samą teraźniejszość. Według przedstawianego modelu to zła interpretacja, ponieważ sonda i Ziemia funkcjonują w różnych czasach odległych o 8 minut. Oczywiście obserwujemy to podczas kontaktu radiowego z sondą, ale nazywamy po swojemu opóźnieniem w transmisji. Z drugiej strony, to co dotąd wytykaliśmy jako błąd, gdy ktoś mówił, że "coś zdarzyło się lata świetlne temu", w pewnym sensie zyskuje poprawność. Właśnie na zasadzie, że nie ma wielkiej różnicy między odległością a czasem. ----------------------------------------------- To nie jest ukończona teoria. Pozostają otwarte pytania: 5. Czy prędkość ekspansji jest zawsze c? Jaki może być związek tej prędkości z grawitacją? Czy dylatacja czasu wywołana grawitacją to zmniejszenie prędkości ekspansji? 6. Jakim sposobem można by hamować ekspansję obiektów? Jak dowolnie poruszać się w przestrzeni 4D? To dałoby niesłychane możliwości, ale też wymagało wielkiej odpowiedzialności. 7. Czy tzw. problem horyzontu można by powiązać z czymś co roboczo nazywam hiperwirem? Chodzi o to, że oddziaływania rozchodzą się po spiralach logarytmicznych. Cofając się w czasie do chwili 0 istnienia wszechświata, droga którą pokonują oddziaływania jest skończona, ale liczba obrotów wokół osobliwości teoretycznie jest nieskończona. Nawet jeżeli fizyka nie lubi nieskończoności, to można tu myśleć o ogromnej liczbie obrotów wokół osobliwości. Czy to mogłoby być przyczyną jednolitego rozkładu temperatury?
-
Ciężka sprawa, skoro nie widzisz różnicy w założeniach i niektórych wnioskach... Wyraziłem to w przystępny sposób i nie mam pomysłu, co jeszcze mogę zrobić. Chyba że chodzi o to, że nie czytałeś od początku albo że było to dawno i zapomniałeś... Wpis na forum jest popularnonaukowy, dlatego posługuję się językiem opisowym i prostą matematyką. Zajmuję się podstawowymi wnioskami, które można w ten sposób wyciągnąć. Czy chciałbym to zmienić? Zasadniczo nie, bo nie tworzymy tu pracy akademickiej. W uzasadnionym przypadku tak - jeżeli wynikną jakieś ciekawe wnioski. Jeżeli zechcesz użyć tensorów, mogę również spróbować podjąć się dyskusji (mam wykształcenie matematyczne). Osobiście nie widzę na tym etapie potrzeby sięgania po takie metody, skoro można prowadzić rozważania przy zredukowanej do 2 liczbie wymiarów. Ale jeżeli Ty widzisz i masz na to czas, to proszę bardzo. Trudno mi ustosunkować się do twoich uwag, gdy piszesz o tożsamości Bianchiego czy ruchu postępowym. Są zbyt lakoniczne. Mógłbyś rozwinąć? I jeszcze zupełnie na marginesie: przypomnę Ci (już to kiedyś wyjaśniałem), że można mieć różne podejścia do wymiany myśli na forum. Ja akurat moje ambicje trzymam w kieszeni. Nie zależy mi na opinii czy sławie. Stawiam na współpracę ludzi i wykorzystanie ich wiedzy. Jeżeli mogę coś wnieść, to wnoszę. Nie prowadzę pojedynków, kto ma rację i kto komu musi coś udowodnić. Możesz mieć inne podejście. Możesz uważać na temat przedstawionej teorii, co chcesz (że jest tożsama, błędna albo sprzeczna z czymś). Fajnie, gdyby przy okazji padły jakieś argumenty. Możesz coś wnosić od siebie albo nie.
-
Pisząc D = ict chodziło mi o to, że redukując wymiary w interwale czasoprzestrzennym do niego dojdziemy. Oczywiście, że czas jest współrzędną. W cytowanym zdaniu miałem na myśli efekty dylatacji czasu (związane z ruchem lub z masą) oraz tzw. "strzałkę czasu". Zbyt duży skrót myślowy. W tej teorii możliwości "manipulowania czasem" są teoretycznie większe. Muszę podkreślić, że ta teoria nie jest tożsama z STW, OTW. Nie można powołując się na te teorie, twierdzić, że zostają powielone już istniejące odkrycia. A z rzeczy niewątpliwie nowych wskażę na proste wyjaśnienie Ciemnej Energii, które tu mamy. Ale są i inne rzeczy, które starałem się wypunktować. Wystarczy uważniej przeczytać. Pracujemy tu na innych założeniach i patrzymy, co z tego wynika. Zaczynamy od najprostszych spostrzeżeń. Jeżeli użycie geometrii różniczkowej da lepszy obraz, to OK. Napisz, jak za pomocą tej techniki wyrazić ten model? Czy doprowadzi to do nowych wniosków? Czekam na forumowiczów, którzy potrafią wnieść coś od siebie do tej teorii albo pokazać kontrprzykład, który ją obali.
-
Dzięki za poprawkę. Faktycznie mogłem gdzieś źle się wyrazić. Kilka uwag o czasie Od początku zakładałem, że czas jest osobnym wymiarem. Można jednak pomyśleć o nim w inny sposób. Mianowicie przyjąć, że czwarty wymiar ma związek z czasem. Używałem już wzoru R=c∙t, gdzie R - promień wszechświata. Przyjmijmy nieco ogólniej: D = c∙t jako związek odległości z czasem. Tym razem chodzi o odległość w 4 wymiarach i na początek (przypadek obiektu nieruchomego w 3D) można przyjąć mierzoną wzdłuż czwartego wymiaru. Nie chodzi tylko o to, że wyraża się tu drogę w ruchu jednostajnym z prędkością c. Można w tym dostrzec związek między pojęciami odległości i czasu. Taka odległość jest równoważna czasowi, podobnie jak energia jest równoważna masie. Zapiszmy to w nieco innej formie: t = D/c I uzyskujemy coś co można by nazwać definicją czasu. Czas dałoby się określić jako zmianę położenia obiektu w czwartym wymiarze wszechświata. Czas byłby w pewnym sensie złudzeniem. Weźmy dowolny nieruchomy obiekt. W omawianym modelu zakłada się, że ten obiekt porusza się z prędkością światła w czwartym wymiarze. A więc w rzeczywistości nie jest wcale nieruchomy, ale z każdą sekundą przesuwa się o 300 000 km. Ale czy należy mówić "obiekt porusza się"? Dotykamy tu już kwestii percepcji i językowych. Percepcji - ponieważ tak postrzegamy ruch, a językowych - ponieważ pojęcie czasu jest mocno wykorzystywane w języku naturalnym. Naturalna percepcja i naturalny język każą nam mówić "obiekt porusza się". Był w punkcie A i po jakim czasie jest w punkcie B. Ale w tym modelu to nie jest dość precyzyjne, chyba nawet niedokładne. Skoro zakłada się, że czas i 4-wymiar są ściśle powiązane, to stwierdzenie "obiekt porusza się" jest bez sensu. To nie jest ruch. Nie można powiedzieć, że obiekt był w punkcie A i po jakimś czasie jest w punkcie B, bo to będzie "masło maślane" - ponieważ odległość od A do B jest tym samym, co czas od A do B. Czas - tak użyteczny w naszej rzeczywistości - jest jako pochodna pojęcia odległości pojęciem nadmiarowym. Wróćmy do naszego nieruchomego w 3D obiektu. Niech to będzie obserwator. Nie można powiedzieć, że porusza się on w czwartym wymiarze. Ustaliliśmy, że ściśle biorąc, nie ma tu żadnego ruchu, a tylko ciąg stanów - od położenia A do położenia B. Żaden z tych stanów nie jest uprzywilejowany. Nie istnieje więc coś takiego jak teraźniejszość. Wielu zdrowo myśląc ludzi zechce temu zaprzeczyć, bo przecież "teraźniejszość jest obserwowana i jest faktem obiektywnym". Owszem, nasza percepcja stworzyła takie pojęcie i jest ono bardzo użyteczne, ale to musi być złudzenie. (Można by bardziej rozwinąć, jak funkcjonuje nasza świadomość, jak działa mózg i jak przyswaja informacje, ale nie będę robił dygresji w tę stronę.) Postawmy kropkę nad i w tych rozważaniach: Również i pojęcia przeszłości i przyszłości są pewną umową przyjętą przez obserwatora. Obserwator nie jest w jednym wybranym położenie na "osi czwartego wymiaru". On jest w wielu położeniach, zaczynając od A do B włącznie. Jest w nich "przez cały czas" (znów widać, że nasz aparat językowy nie jest dostosowany, aby to precyzyjnie wyrazić). Nie jest tak, że "kiedyś" był w położeniu A, a "później" znalazł się w położeniu B. Podkreślę: jest niejako we wszystkich tych położeniach "jednocześnie". Ale obserwator był dowolny. To samo można powiedzieć, o dowolnym nieruchomym obiekcie, a także z dobrym przybliżeniem o dowolnym wolno poruszającym się obiekcie (wolno w porównaniu do prędkości światła). Co by więc z tego wynikało? Ano to, że stan wszechświata w przeszłości nie jest czymś co "znikło", definitywnie przeminęło. A stan w przyszłości jest czymś "nieistniejącym", nieokreślonym. W OTW mamy: D = i∙c∙t gdzie i jest jednostką urojoną. Wzór jest podobny, ale jednak inny. W szczególności trudno podać jego interpretację fizyczną, ponieważ stała "i" ma interpretację czysto matematyczną. Inne są również wnioski z obu teorii. W OTW czas jest wielkością skalarną, a więc płynie (wolniej lub szybciej) w jednym kierunku. Natomiast w rozważanym modelu przyjmuje się, że czwarty wymiar jest taki sam jak trzy pozostałe, a jego wybór może się zmieniać. Oczywiście, nie na zasadzie abstrakcyjnego wyboru układu odniesienia, ale mówiąc w skrócie poprzez wybór kierunku "ruchu" obserwatora. Chodzi mi o to, co starałem się przedstawić na tym rysunku: Dowolny ruch w 3D modyfikuje kierunek czwartego wymiaru. Oczywiście, przy prędkościach małych w porównaniu do c, efekty są mało zauważalne. Co najwyżej przekładają się na coś, co obserwujemy jako małe dylatacje czasu. Teoretycznie istnieje jednak możliwość dużej zmiany. Posłużę się jeszcze raz naszymi naturalnymi pojęciami i językiem, bo nie za bardzo mam inny wybór. Wyobraźmy sobie wszechświat jako ekspandującą w czwartym wymiarze materię. W omawianym modelu nic nie stoi na przeszkodzie, aby zmieniać kierunek ekspansji wybranego obiektu lub obserwatora. Istnieje możliwość dowolnego "pływania" w całej przestrzeni 4-wymiarowej, o ile uda się zmienić kierunek.
-
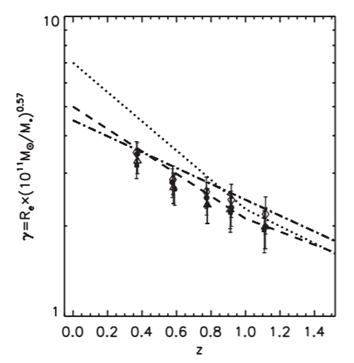
Jeżeli chodzi o efekty relatywistyczne w prezentowanym modelu, to można stwierdzić, że wzory STW obowiązują, ponieważ układ jest inercjalny. Ruch w 4. wymiarze jest jednostajny. Wcześniejsze wywody opierały się ilustracji, na której prezentowano ruch z perspektywy poruszającego się obiektu (a nie w statycznym układzie współrzędnych). Podtrzymuję jednak zdanie, że najprawdopodobniej zawierają błędy. Nie zajmowałem się tym, więc znalezienie nowych praw fizycznych pozostawiam zainteresowanym. ----------------------------------------------- Wracając do samego kosmosu. Do tej pory opisałem 3 argumenty obserwacyjne za wyprowadzonym wzorem na wzrost odległości wraz z czasem (d(T+t)=d(T)*(1+t/T)): a) im dalej położone są galaktyki, tym szybciej się oddalają b) im starsze są galaktyki, tym są większe c) odległość Księżyca od Ziemi zwiększa się Argument b) był opisany w innym wątku. Przytoczę go tutaj, nieco dokładniej prezentując wyniki: Czy ekspansję wszechświata stwierdzono wewnątrz galaktyk? Pewne wnioski można wyciągnąć na podstawie wyników pracy "The evolution of the mass–size relation for early-type galaxies from z ∼ 1 to the present: dependence on environment, mass range and detailed morphology" (https://academic.oup.com/mnras/article/428/2/1715/1009056). Popatrzmy na Figure 9 z tej pracy: Wykres 9. Unormowane masą promienie galaktyk o masach jako funkcja przesunięcia ku czerwieni dla różnych wyborów w porównaniu do dawniej publikowanych wyników Na osi X zaprezentowano przesunięcie ku czerwieni, czyli de facto wiek obiektu. Duże przesunięcie oznacza odległe obiekty, obserwowane w młodym wszechświecie. Na osi Y odnotowano promień galaktyki unormowany jej masą. Wykres pokazuje, że początkowo galaktyki były mniejsze. Taki wynik można tłumaczyć na różne sposoby. Autorzy pracy wskazują na możliwość łączenia się galaktyk, co powodowałoby wzrost promienia. Oczywiście, do łączenia czasem dochodzi, ale zasadniczo galaktyki się "rozbiegają", więc o nieustanne łączenie trudno. Drugim tłumaczeniem jest utrata masy, np. poprzez wiatr gwiezdny lub dżety kwazarów. I to również jest fakt, pytanie tylko, czy w ten sposób można wytłumaczyć całkowitą zmianę wielkości. Wzór na przyrost odległości mógłby posłużyć jako dodatkowe wyjaśnienie. W każdym razie obserwacje i wzór nie stoją w sprzeczności. Odczytajmy z wykresu promienie i z w zaznaczonych punktach, wypisując je zgodnie z upływem czasu (czyli od największych przesunięć z do najmniejszych): z gamma wiek t d(T) * (1 + t/T) 1,1 2,2 5,5 0 2,2 0,9 2,4 6 0,5 2,4 0,8 2,7 6,8 1,3 2,7 0,6 3,0 8 2,5 3,2 0,4 3,6 9,4 3,9 3,8 Dwie pierwsze kolumny to wartości z wykresu. Wiek galaktyk jest wyliczony na podstawie z. Pierwszy punkt obserwacji określa czas T=5,5 mld lat. Czas t będzie liczony od tego momentu. Początkowa wielkość to d(T)=2,2. W ostatniej kolumnie wpisano wynik obliczeń wielkości za pomocą wzoru. Jak widać, użycie wzoru na przyrost odległości daje wyniki zadziwiająco podobne do obserwowanych. Niemniej należy pamiętać, że to tylko wyniki szacunkowe oraz że w normowaniu masą występuje potęga 0.57. Nie uwzględniono również czynników wymienionych przez autorów pracy.
-
Masz rację, coś tu nie gra. Za bardzo się pośpieszyłem, bo rzeczywiście obrazek dla fotonu nie odpowiada rzeczywistości. Foton powinien być obserwowany w pkt docelowym w późniejszym czasie, a nie natychmiast. Wpis o ruchu jest błędny i wymaga poprawienia.
-
O bezwładności i sile odśrodkowej
Jaglo odpowiedział(a) na Jaglo temat w Astrofizyka, kosmologia i teorie
Tego nie rozumiem. Według mnie to dwa różne rozkłady masy. Czy to nie za duże przybliżenie? Czy mógłbyś nieco objaśnić, jak wyliczyłeś potencjał? Zignorowanie G i bezwzględnej wartości M rozumiem. Zamianę dm(r) na 1/r dr również. Ale nie wiem, w jaki sposób scałkowałeś obszar po R2. Tak na moje wyczucie całka powinna być oznaczona. Również fajnie by było, gdybyś wyjaśnił co nazwałeś 'z'. Gdy już zrozumiem to od strony fizycznej, to może pojmę od matematycznej tę operację, gdy całkujesz i po chwili różniczkujesz po r. Wyszło "masło maślane", pewnie dlatego że całka była nieoznaczona... Wreszcie sam wynik v=1 (ogólnie mówiąc const) jest nieco podejrzany z praktycznego punktu widzenia. Dla małych r obserwuje się mniejszą prędkość ruchu, co przy poprawnych założeniach i obliczeniach nie powinno się zdarzyć. A wyważaniu powtarzasz kolejny raz, więc muszę to skomentować. Gdyby drzwi były otwarte i nie było żadnych problemów, nikt by nie wymyślał Ciemnej Materii. W przypadku galaktyk spiralnych przypadek jest tak oczywisty, że dziwię się, że próbujesz klasycznym wzorem uzgodnić się do obserwacji. Oczywiście, próbuj, chętnie zobaczę Twoje sposoby na rozwiązanie tego problemu. A ponieważ są i kolejne "zarzuty", to i na nie odpowiem. Co do obalania Einsteina - nic nie próbuję obalić. Pokazałem tylko, co się stanie, gdy abstrakcyjny układ odniesienia zastąpi się fizycznym. Reszta to fizyka Newtona, którą można stosować przy małych prędkościach. Co do całkowania numerycznego - nie wiem, gdzie się tego dopatrzyłeś. Pewnie to przejęzyczenie i chodziło o dyskretyzację i późniejsze rozwiązywanie układu równań. To metody dobre jak każde inne, coś pośredniego między wyliczeniem analitycznym a symulacją. A że nie tak proste - cóż, a czy wszystko musi dać się wyrazić analitycznie? A gdybym to zapisał macierzami i wektorami to byłoby krócej, ale czy bardziej poprawnie? A co do zadawania filozoficznych pytań - zasadniczo zadawanie pytań uznaję za zaletę. A gdy nie ma gotowych odpowiedzi, to nie nazywałbym tego filozofią, tylko dociekaniem. Oczywiście Tobie się wydaje, że wszystko można wyjaśnić na gruncie poznanych teorii. Gdyby tak było, w astronomii nie byłoby zgrzytów typu Ciemna Materia i Ciemna Energia, a fizycy teoretyczni zaprzestaliby swoich prac na nowymi teoriami. Skoro już znalazłeś, to zacytuj proszę. Co do określeń typu "pisanina" (a wcześniej "filozofowanie" w znaczeniu pejoratywnym), to prosiłbym, abyś się zastanowił nad szafowaniem nimi. Rozumiem, że jesteś bardzo przekonany do swego i to okazujesz poprzez takie emocjonalne epitety, ale to merytorycznie nic nie wnosi, a zasadniczo zniechęca mnie do odpowiadania. A co do niezrozumienia, to polecam zapytać. Chętnie odpowiem. lkosz Gdyby była taka możliwość, to zastanowiłbym się, czy tak zrobić. W moim tekście te pojęcia nie występują. Wychodzę od prostych założeń, a potem rozważam coraz bardziej złożony układ ciał. To normalne postępowanie przy każdym modelowaniu. Czy to nazwałeś przybliżaniem, czy widzisz jakąś matematyczną niedokładność, czy dopatrzyłeś się czegoś innego? Jeżeli coś robię źle, to prosiłbym o konkretne wskazanie miejsca, gdzie występuje jakieś niewłaściwe przybliżenie. "Machasz rękoma" to określenie uzasadniania czegoś bez dowodu. Ja natomiast nie twierdzę, że coś udowodniłem, tylko zachęcam do dokładniejszego sprawdzenia. Mógłbyś sprecyzować, co uważasz za zbytnie uproszczenie? Nie, no, nie przesadzajmy, że fizyka Newtonowska jest błędna koncepcyjnie Ale tak poważnie, to obliczenia z użyciem potencjału grawitacyjnego to niby jaka fizyka? Jeżeli wyklarujesz, gdzie widzisz uproszczenia to porozmawiamy. Te grawitony to nie mój pomysł, a nawet gdyby mój to nie tak się ocenia koncepcje, że określisz coś jako "nadużycie" i "szafa gra". Konkrety proszę. Nawet jeżeli to nie grawitony miałyby decydować, to nie są one podstawą obliczeń. Ich udział można zastąpić innym wyjaśnieniem, całość wyliczeń pozostawiając bez zmian. No tak, "stare" koncepcje Newtona są bezużyteczne Co do "wydajęmisię bez dowodów" to wyraźnie zaznaczam, że to wszystko hipotezy, więc Ameryki nie odkrywasz tym komentarzem. Którego? Takie to dwuznaczne, że aż się uśmiechnę Ale generalnie dziękuję za zainteresowanie i uwagi. -
O bezwładności i sile odśrodkowej
Jaglo odpowiedział(a) na Jaglo temat w Astrofizyka, kosmologia i teorie
Rozpisuję się i kombinuję po to, aby było zrozumiałe. Nie wszyscy muszą rozumieć skomplikowane wzory, więc w miarę możliwości ich unikam i zastępuję opisem. Co do błędów to co konkretnie masz na myśli? Sugerujesz, że wystarczy zmienić rozkład masy w galaktykach i wszystko będzie się zgadzać? To jasne, tyle że rozkład materii jest jaki jest, a gdy chcemy go zmodyfikować, musimy wprowadzić coś ekstra, czego nie widzimy. Ciemna Materia to póki co hipoteza, chociaż popularna to jednak nieudowodniona. Celowo wybieram inne podejście. -
O bezwładności i sile odśrodkowej
Jaglo odpowiedział(a) na Jaglo temat w Astrofizyka, kosmologia i teorie
W tym fragmencie kodu: else if (i<n) a[n,i] = -m[]/r[n]/Mcalk else if (i>n) a[n,i] = -m[]*r[n]/r[]^2/Mcalk zgubiły się indeksy i. Widocznie i w nawiasie prostokątnym to jakieś specjalne formatowanie wpisu. Aha, już widzę, to robi italic -
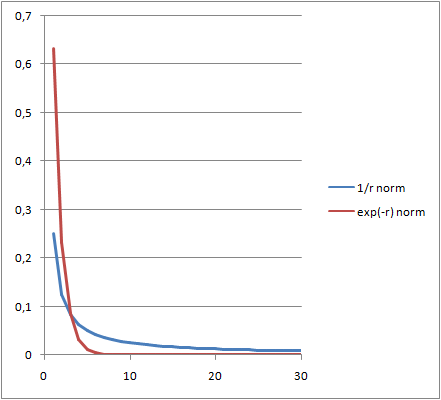
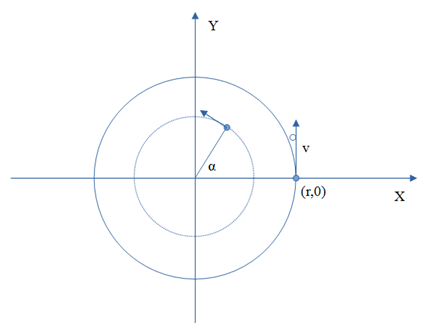
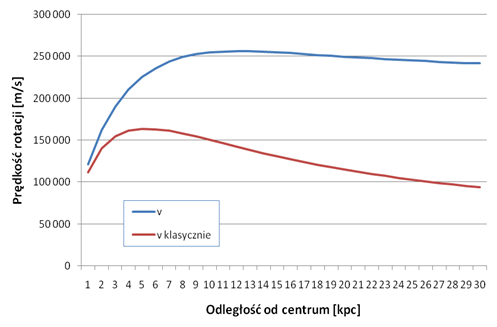
Czym jest bezwładność wiemy intuicyjnie. Gdy samochód rusza, jakaś siła wciska nas w fotel. Gdy hamujemy, jakaś siła powoduje, że lecimy do przodu. Fizyka posługuje się tym pojęciem nie od dziś. Czy można tu odkryć coś nowego? Zobaczmy. Jak na forum astronomiczne przystało, zajmiemy się obiektami kosmicznymi. W układzie dwóch ciał (np. Słońce - Ziemia) bezwładność definiuje orbitę mniejszego z ciał. Na Ziemię działa siła ciążenia, która ciągnie ją ku Słońcu. Ale też Ziemia jest w ruchu, co wywołuje siłę odśrodkową. Tu właśnie wkracza bezwładność. Skąd się bierze siłą odśrodkowa? Co się za nią kryje? Aby obliczyć wartość siły odśrodkowej w układzie dwóch ciał, należy rozważyć krótki przyrost czasu i porównać położenie ciała rzeczywiste (czyli na orbicie) z położeniem w sytuacji, gdyby ciało poruszało się bezwładnie (czyli po prostej). Różnica pozycji określi drogę, a z niej wyniknie jakie przyśpieszenie odśrodkowe działa na ciało. Otrzymamy: a = v2/r. Siła odśrodkowa wynosi m*a, czyli: F = m*v2/r To jest klasyczny wynik. Taki wzór wielokrotnie był stosowany do obiektów kosmicznych. Można go stosować do układów planetarnych i księżycowych i sprawdzi się doskonale. Ale jest jeszcze jeden typ układów, w których mamy do czynienia z ruchem po orbicie, i w którym dzieje się coś zagadkowego. Mam na myśli galaktyki spiralne. Tradycyjne podejście polegające na porównaniu siły ciążenia z siłą odśrodkową w ich przypadku zawodzi. Po uwzględnieniu rozkładu mas widocznych obiektów, z równania można wyliczyć prędkość. I ta prędkość wychodzi zbyt mała w porównaniu z tym co wynika z obserwacji. Co więcej prędkość ruchu gwiazd według równania maleje wraz ze wzrostem odległości od centrum galaktyk. A tymczasem w rzeczywistości powyżej danej granicy obserwuje się niemal stałą wartość prędkości. O co chodzi? Czyżby siła ciążenia była większa niż wyznaczamy? Wydaje się że tak, bo inaczej gwiazdy zostałyby wyrzucone z galaktyk, wirując tak szybko. Czy w galaktykach występuje Ciemna Materia, której nie widać (nie wysyła promieniowania świetlnego ani radiowego), a oddziałuje grawitacyjnie, trzymając galaktyki spiralne w całości? Niewykluczone, zwłaszcza że na jej trop, w postaci efektu soczewkowania grawitacyjnego, natrafia się w galaktykach eliptycznych. Najbardziej znany przykład to galaktyka Pocisk. Ale rozważmy jeszcze inną możliwość. Mamy równanie równowagi sił grawitacji i odśrodkowej: Fg = Fo Jedna możliwość to zwiększenie siły grawitacji poprzez dodanie Ciemnej Materii, ale jest i druga możliwość - zmniejszenie siły odśrodkowej. Niby czemu mielibyśmy to zrobić? Na jakiej zasadzie? Zasada będzie prosta. Gdy patrzymy na galaktykę spiralną, w jaki sposób wyznaczamy prędkość orbitalną? Oczywiście, ustalamy układ współrzędnych, którego środek znajduje się w centrum galaktyki, a osie celują w odległe obiekty (inne galaktyki). Jest to poprawne matematycznie i bardzo wygodne podczas obliczeń. Jednak czy nie kryje się w tym błąd, polegający na zbytnim abstrahowaniu od rzeczywistości fizycznej? De facto mierzymy prędkość orbitalną względem odległych galaktyk. A jaki związek ma np. Słońce z odległymi galaktykami? Wydaje mi się, że niezbyt wielki. Jeżeli chodzi o oddziaływania, czy nie powinniśmy się skupić na naszym najbliższym otoczeniu? Zwłaszcza jeżeli chodzi o oddziaływanie grawitacyjne, dużo większe znaczenie mają sąsiednie gwiazdy niż odległe galaktyki. Czy nie powinno się mierzyć prędkości względem sąsiednich gwiazd? Czy układem odniesienia nie powinny być fizyczne obiekty, a nie abstrakcyjny układ współrzędnych? Słońce orbituje wokół centrum Drogi Mlecznej z prędkością 220 km/s. Ale w stosunku do najbliższych gwiazd prędkość nie jest aż tak duża, bo sąsiednie gwiazdy też poruszają się szybko. Lecimy więc szybko, czy może wcale nie? Wybierzmy to inne podejście i zobaczmy do czego nas zaprowadzi. Przyjmijmy mianowicie, że ruch ciał będziemy określać wyłącznie względem obiektów fizycznych. Oczywiście będą nas interesowały duże obiekty (takie jak gwiazdy), a nie małe obiekty czy pyłki kosmiczne. Przyjmijmy ogólnie zasadę, że nasze "zainteresowanie" będzie proporcjonalne do masy obiektu. Drugie założenie: obiekt interesuje nas tym bardziej, im bliżej się znajduje. Odległe galaktyki nas nie interesują, bliskie gwiazdy tak. Ogólnie, "zainteresowanie" będzie odwrotnie proporcjonalne do kwadratu odległości. Mamy więc dwa założenia - decyduje masa podzielona przed odległość do kwadratu - identycznie jak w prawie powszechnego ciążenia. Jaki mechanizm fizyczny miałby stać za takim rozwiązaniem? Stawiałbym na... grawitony. Moim zdaniem grawitacja to nie tylko odkształcenie czasoprzestrzeni, ale też wymiana cząstek elementarnych między obiektami. Cząstek jeszcze nieodkrytych - właśnie grawitonów. W naszym klasycznym podejściu traktujemy siłę grawitacji rotującej galaktyki jako statyczną (pomijając nieregularności wynikające z tego, że istnieją ramiona galaktyki). Gdy gwiazdy we wnętrzu galaktyki spiralnej się przesuną, na ich miejsce pojawiają się nowe podobne. Wydaje się więc, że w układzie nic się nie zmieniło. Siła ciążenia wydaje się niezmieniona. Gdy jednak pomyślimy, że grawitacja to również oddziaływanie cząstek elementarnych, to dostrzeżemy, że układ jest dynamiczny. Gwiazdy są w ruchu, a więc i grawitony są w ruchu. Pole grawitacyjne jest w ruchu. I to może być uzasadnieniem dla tego, aby wiązać układ odniesienia z materią, która to pole generuje. Spróbujmy zastosować to podejście w praktyce. Zacznijmy od najprostszego przypadku dwóch ciał w ruchu. Ciało pierwsze znajduje się w odległości r od środka układu współrzędnych, a drugie w odległości s. Ich prędkości to v(r) i v(s). Rozważmy dwie sytuacje dotyczące pierwszego ciała: a) ciało krąży po rzeczywistej orbicie, b) ciało porusza się ruchem bezwładnym. Ale tym razem układ odniesienia zwiążemy z ciałem krążącym po mniejszej orbicie. Po transformacji układu współrzędnych i prędkości, ruch bezwładny będzie przebiegał inaczej niż w poprzednim układzie z ciałem centralnym. Ciało pierwsze nie poleci pionowo w górę, ale przesunie się nieznacznie w kierunku centrum, "podążając" z ciałem z mniejszej orbity. Teraz przyśpieszenie wyraża się wzorem: a = v(r)2/r - v(s)2/s*cos(α) Przyśpieszenie odśrodkowe działające wzdłuż osi X jest pomniejszone o czynnik v(s)2/s*cos(α). Idźmy dalej i rozważmy jednorodny pierścień ciał orbitujących z tą samą prędkością po mniejszym z okręgów. Aby wyliczyć przyśpieszenia działające na pierwsze ciało, należy uwzględnić wszystkie obiekty z mniejszej orbity, a więc kąty α od 0 do 360 stopni. Ale gdybyśmy to zrobili na wprost, to przyjęlibyśmy, że każdy obiekt orbity jest jednakowo ważny. Wynik nie zależałby od wielkości ciał ani odległości od nich. Jeżeli chodzi o masę, to przyjęliśmy, że pierścień ciał jest jednorodny. Każde ciało ma więc tę samą masę. Masę można więc pominąć. Ale już odległości ciała dalszego od poszczególnych elementów pierścienia są różne. Można je obliczyć i uwzględnić przy wyznaczaniu wypadkowej siły odśrodkowej względem ruchomego pierścienia. Będziemy wyznaczać średnie ważone czynnikiem 1/d2 przyśpieszenie dla poszczególnych elementów pierścienia. Co to znaczy? To znaczy, że każdy element pierścienia będzie stanowił punkt odniesienia, czyli początek układu współrzędnych. A wynik będzie uśredniony. Dlaczego tak? Otóż w omawianym przypadku nie ma innych obiektów niż ciała na mniejszej orbicie. Względem nich porusza się ciało 2 i tylko względem nich można określać ruch ciała 1. Siła odśrodkowa dla ciała na orbicie o promieniu r względem ruchomego pierścienia ciał znajdujących się na orbicie o promieniu s wynosi: a(s) = (v(r)2 - v(s)2)/r, jeżeli s<r A jeżeli pierścień wiruje na zewnątrz (czyli s>r), to wychodzi: a(s) = v(r)2/r - v(s)2/s2*r Jak widać, znów otrzymaliśmy wzór, w którym występuje klasyczne wyrażenie v(r)2/r, i znów wartość jest pomniejszona. Kiedy już to mamy, możemy wyobrazić sobie wiele pierścieni, każdy wirujący z własną prędkością i każdy posiadający dowolną masę: Przy wyznaczaniu przyśpieszenia dla ciała na orbicie o promieniu r będziemy analogicznie jak poprzednio ważyć przyśpieszenia poszczególnych pierścieni, tym razem ich masą, aby uwzględnić ruch pola hipotetycznych grawitonów. Ze względu na wygodę obliczeń zastosujemy podejście dyskretne. Powiedzmy, że mamy N pierścieni o promieniach r1, r2... rN i o masach odpowiednio m1, m2... mN, poruszających się z prędkościami v1, v2... vN. Wówczas przyśpieszenie obliczone będzie jako: a = suma[ m(i)*a(s(i)) dla i=1..N ] / suma[ m(i) dla i=1..N ] Na tym się zatrzymajmy. Nie będę już bardziej urealniał tego przypadku, dodając ramiona galaktyki, ponieważ byłoby to zbyt skomplikowane. O ile znamy odległości i masy obiektów wirującego dysku, to otrzymany wzór można wykorzystać do obliczenia prędkości z jaką pierścienie wirują. W tym celu należy ułożyć układ równań, gdzie przyśpieszenie odśrodkowe każdego pierścienia przyrówna się do przyśpieszenia grawitacyjnego. a(r1) = b(r1) a(r2) = b(r2) ..... ..... ..... a(rN) = b(rN) gdzie b(r) oznacza przyśpieszenie grawitacyjne na orbicie r. W tym układzie równań współczynnikami są promienie i masy, a niewiadomymi prędkości. Okazuje się, że jest to układ równań liniowych ze względu na każde v2. Można go rozwiązać, a z otrzymanego wyniku wystarczy wyciągnąć pierwiastek, aby otrzymać prędkości v poszczególnych pierścieni. Zobaczmy jak go zastosować w praktyce. Przykładowo, przyjmijmy założenia na podobieństwo parametrów Drogi Mlecznej: - masa całkowita wszystkich pierścieni to 6e10 mas Słońca, - masa Słońca 2e30 kg, - promień wirującego dysku 30 kpc, - gęstość materii w zależności od odległości od centrum proporcjonalna do exp(-r/3), gdzie promień jest w kpc. Oczywiście użyjemy stałych astronomiczno-fizycznych: - kiloparsek 3e19 m, - stała grawitacyjna G 6.67e-11 m3/kg/s2. Dodatkowo przyjmijmy, że twierdzenie Newtona o warstwach, prawdziwe dla kul w 3D, będzie z grubsza działać w 2D. Ze względu na bardzo grube założenia o rozkładzie masy nie ma sensu liczyć przyśpieszenia grawitacyjnego dokładniej. Tworzymy 30 pierścieni, a więc układ 30 równań i rozwiązujemy. Można to zrobić np. takim kodem w języku R: Oznaczenia: N - liczba pierścieni, r - promienie w metrach, m - masy pierścieni, M - masa dysku o danym promieniu (suma mas pierścieni do danego promienia), Mcalk - masa całkowita wszystkich pierścieni. Tabela z danymi i obliczonymi prędkościami: nr r [m] m [kg] v [m/s] 1 3E+19 5,62E+39 121 035 2 6E+19 1,21E+40 162 261 3 9E+19 1,44E+40 190 299 4 1,2E+20 1,45E+40 210 619 5 1,5E+20 1,33E+40 225 529 6 1,8E+20 1,17E+40 236 385 7 2,1E+20 9,89E+39 244 130 8 2,4E+20 8,18E+39 249 480 9 2,7E+20 6,64E+39 252 999 10 3E+20 5,32E+39 255 137 11 3,3E+20 4,21E+39 256 250 12 3,6E+20 3,3E+39 256 617 13 3,9E+20 2,57E+39 256 453 14 4,2E+20 1,99E+39 255 923 15 4,5E+20 1,53E+39 255 150 16 4,8E+20 1,17E+39 254 225 17 5,1E+20 8,95E+38 253 214 18 5,4E+20 6,8E+38 252 164 19 5,7E+20 5,15E+38 251 108 20 6E+20 3,89E+38 250 068 21 6,3E+20 2,93E+38 249 059 22 6,6E+20 2,2E+38 248 089 23 6,9E+20 1,65E+38 247 164 24 7,2E+20 1,24E+38 246 286 25 7,5E+20 9,24E+37 245 454 26 7,8E+20 6,89E+37 244 669 27 8,1E+20 5,13E+37 243 929 28 8,4E+20 3,81E+37 243 230 29 8,7E+20 2,83E+37 242 572 30 9E+20 2,1E+37 241 951 Otrzymano prędkość ok. 250 km/s. Jak wspominałem prędkość Słońca, znajdującego się w odległości ok. 8 kpc od centrum Galaktyki, według pomiarów wynosi 220 km/s. Różnica może być wytłumaczalna niedokładnością danych i uproszczeniami. Na tych danych przeprowadzając obliczenia metodą klasyczną z równania Fg = Fo, otrzymamy ok. 160 km/s, czyli za mało. A tak wypada proponowana metoda wyliczania prędkości w porównaniu do klasycznej na wykresie: Otrzymane prędkości dają płaski przebieg, podczas gdy przy klasycznym podejściu prędkości maleją wraz z odległością, co jak wspomniałem kłóci się z obserwacjami astronomicznymi. Możliwe więc, że zaprezentowane podejście do bezwładności da wyniki bardziej zgodne z obserwacjami dla galaktyk spiralnych. To wymaga dalszych sprawdzeń z wykorzystaniem dokładniejszych danych. Podsumowując: zastosowano tu uogólnioną zasadę ruchu bezwładnego. Jeżeli rozważamy układ dwóch ciał - centralnego i orbitującego - to wybiera się jeden układ współrzędnych ze środkiem w centrum. W takim przypadku proponowana metoda ważenia układów odniesienia masą i odległościami nic nie zmienia, bo jest tylko jedna masa i jedna do niej odległość. (Średnia ważona z jednej wartości to dokładnie ta wartość.) Jeżeli jest wiele ciał - jak w przypadku galaktyk - stosuje się wiele punktów odniesienia, względem których wyznacza się ruch bezwładny. Wówczas przyśpieszenie odśrodkowe jest ważoną wypadkową przyśpieszeń względem wszystkich ciał, a wagi odpowiadają natężeniu pól grawitacyjnych generowanych przez te ciała. Zastosowany opis matematyczny na tę chwilę jest tylko hipotezą.
-
A to dobrze że irracjonalne Tylko w ten sposób dokonuje się postęp Twierdzenie, że nasza rzeczywistość jest 3D może być takim samym uproszczeniem, jak zdroworozsądkowe twierdzenie że Ziemia jest płaska, bo przecież widać, że się nie zagina. Rozważania, które przedstawiłem, i tak są umiarkowanie irracjonalne. Teoria strun operuje w 11 wymiarach... Ruch po osi pionowej to dla nas nie jest ruch, tylko spoczynek. Ruch w przestrzeni zilustrowałem na osi poziomej. I wtedy ruch z prędkością v leci na ukos. A foton porusza się dokładnie poziomo, ponieważ jest ograniczenie na prędkość światła i składowa pionowa wynosi zero. Natomiast 45 stopni osiąga się przy mniejszej prędkości. Podobieństwo teorii sformułowanych na ten sam temat jest nieuniknione. Jednak przyjmuję zupełnie inne założenia: w opisanej propozycji czas tyka w tle, a przestrzeń de facto jest 4D. Nie łączy się czasu z jedną wybraną osią, on działa na wszystkie 4 osie przestrzeni. Przyznam, że sam miałem kiedyś wrażenie, że ten model można zredukować do klasycznej czasoprzestrzeni i że 4 wymiar przestrzenny jest niepotrzebny. Na tę chwilę jestem zdania, że ten wymiar to będzie coś innego niż czas. Dopóki nie widzę luk w tej teorii, będę ją próbował rozwinąć
-
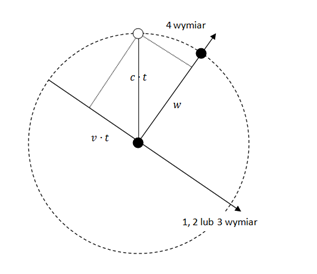
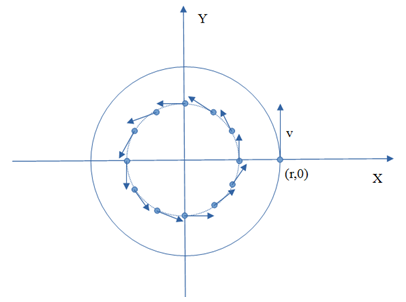
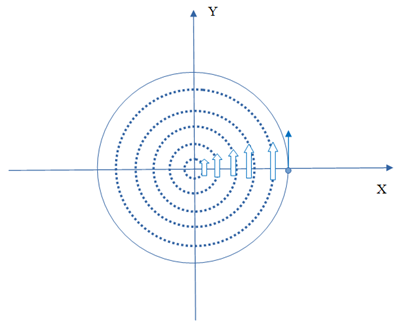
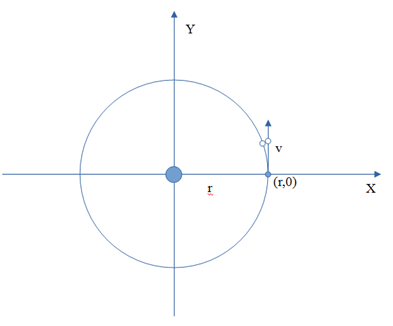
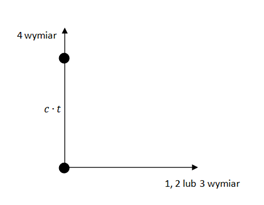
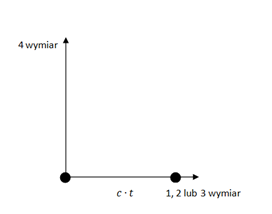
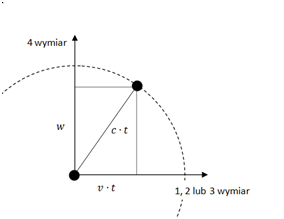
Co można powiedzieć o ruchu we wszechświecie 5D? Jak wskazywałem powyżej, każde ciało porusza się w czwartym wymiarze przestrzennym z prędkością światła. Jeżeli przyjmiemy za punkt odniesienia naszą kanapę, prędkość w 3D wynosi 0, ale i tak poruszamy się z zawrotną prędkością w dodatkowym wymiarze. Można to zilustrować w następujący sposób: Na osi X prezentujemy jeden z wymiarów 3D, na osi Y czwarty wymiar. Ciemna kropka reprezentuje nas na kanapie. W chwili 0 jesteśmy w położeniu (0,0), a po czasie t w położeniu (0,c*t) - tam gdzie druga kropka. Nie przesunęliśmy się w lewo ani w prawo, co właśnie oznacza, że nasz ruch w 3D nie nastąpił. Przesunęliśmy się wyłącznie w górę, ekspandując razem z całym wszechświatem. Teraz drugi skrajny przykład. Włączamy lampę w pokoju i puszczamy w ruch światło. Na obrazku wygląda to tak: Tym razem kropka oznacza foton. W chwili 0 jest on w naszym pokoju w pozycji (0,0), a po czasie t oddala się od nas do położenia (c*t,0) - czyli wzdłuż osi X. Odległość między kropkami wynosi dokładnie c*t, gdzie c to oczywiście prędkość światła. Co ciekawe, nie obserwujemy ruchu w 4 wymiarze. A dlaczego? Popatrzmy na kolejny przykład. Sytuacja pośrednia - ruch z pewną prędkością v: Osie pozostają bez zmian. Punkt startuje z początku układu współrzędnych, ale tym razem porusza się w 3D z prędkością v. W obu poprzednich przykładach widzieliśmy, że po czasie t obiekt pokonuje drogę długości c*t. I tym razem nie jest inaczej. W zależności od v punkt znajdzie się gdzieś na okręgu o promieniu c*t. Po czasie t przebędzie drogę równą v*t wzdłuż wymiaru przestrzeni 3D oraz pewną drogę (na obrazku oznaczoną "w") wzdłuż czwartego wymiaru. Widzimy już, że spoczynek i ruch z prędkością światła to tylko szczególne przypadki tego, co ilustruje obrazek 3. Cechą wspólną wszystkich jest to, że każdy obiekt jest w ruchu i porusza się z prędkością c, a prędkość v to jedynie rzut tego faktu na przestrzeń trójwymiarową. Jeżeli już narysowałem trójkąty prostokątne, to pozwolę sobie wykonać krótkie obliczenia a'la Pitagoras: w2 + (v*t)2 = (c*t)2 Stąd odległość w: w = [(c*t)2 - (v*t)2]0.5 Podzielmy obie strony przez c, a otrzymamy wzór na upływ czasu dla ciała z ilustracji: t* = t * [1 - (v/c)2 ]0.5 Otrzymaliśmy wzór na dylatację czasu dla ciał w ruchu, taki sam jak w Szczególnej Teorii Względności. Popatrzmy jeszcze raz na obrazek nr 2. Dla obiektu poruszającego się z prędkością światła, czas wydaje się nie płynąć. Foton nie przesunął się w górę osi Y. Na obrazku nr 3 obiekt przesunął się w górę osi Y, ale nie tak daleko jak na obrazku nr 1. To mniejsze przesunięcie oznacza właśnie, że z perspektywy układu XY - czyli nas na kanapie - czas poruszającego się obiektu płynie wolniej niż nasz czas. To właśnie wyraża otrzymany wzór. Im większe v, tym mniejsza wartość t* (upływu czasu poruszającego się obiektu). Ale to w pewnej mierze można nazwać złudzeniem. W każdym z przykładów promień drogi, po którym porusza się ciało, jest tej samej długości. Lecąc rakietą po drodze od pierwszej do drugiej kropki mamy zawsze tyle samo czasu, tj. t. No dobrze, czas poruszającego się obiektu płynie wolniej, zróbmy zatem takie hokus-pokus: Punkty na obrazku nr 4 zostały w tych samych położeniach. Zmieniło się tylko położenie osi XY, które przekręciłem w ten sposób, aby oba punkty leżały na osi Y. W zmienionym układzie odniesienia obiekt jest w spoczynku tak samo, jak na obrazku nr 1. Co to oznacza w praktyce? Powiedzmy, że wcześniej staliśmy na ulicy i patrzyliśmy na przejeżdżający z prędkością v samochód. Teraz siedzimy w samochodzie i mówimy, że to jest nasz układ odniesienia. Pozostajemy w spoczynku względem siedzenia samochodu, a świat za szybą porusza się z prędkością v, zostając za naszymi plecami. Ten umykający świat symbolizuje biała kropka na rysunku. OK, zmienił się układ odniesienia i tyle. Popatrzmy jednak uważnie na rysunek. Znów można narysować trójkąty Pitagorasa. I znów można przeprowadzić obliczenia i dostać: t* = t * [1 - (v/c)2 ] Niby nic niezwykłego. Ale przypominam, że teraz świat na zewnątrz samochodu porusza się z prędkością v. To czas tego świata płynie wolnej niż w samochodzie. Tak , to nie pomyłka. W przykładzie 3 staliśmy na chodniku i widzieliśmy, że czas w samochodzie płynie wolniej niż nasz, a w przykładzie 4 jedziemy samochodem i widzimy, że czas na ulicy płynie wolniej niż nasz. Taki "paradoks". O co chodzi? Osoby znające Szczególną Teorię Względności nie będą zaskoczone. STW opisuje takie same efekty. Rzućmy drugie uważne spojrzenie na ostatni obrazek. Osie się przekręciły. Co to oznacza? Wpierw mieliśmy przestrzeń wzdłuż OX, a upływ czasu wiązał się z OY. Teraz mamy jakby sytuację pośrednią i pomieszanie tych pojęć. Przestrzeń jest w inną stronę i jakby zachodzi na upływ czasu. A upływ czasu zachodzi na przestrzeń. Krótki wtręt. Co to są kierunki? Na Ziemi odróżniamy wschód-zachód, północ-południe i góra-dół. Ale w kosmosie nie ma takich rzeczy. Wszystko jest umową (na Ziemi zresztą też). Nie jest tak, że pierwszy wymiar to jakiś konkretny kierunek w kosmosie, wycelowany w jakąś gwiazdę lub galaktykę. Podobnie z drugim i trzecim wymiarem. W kosmosie jest pełna swoboda. Jak wybierzemy - tak będzie. Układ współrzędnych jest umowny. Wracając do przykładu nr 4 - widzimy coś podobnego, ale jeszcze ciekawszego. To co w jednym układzie jest przestrzenią, w innym układzie zamienia się w upływ czasu wzdłuż czwartego wymiaru. Kiedy pomyślimy chwilę, to dojdziemy do wniosku, że czwarty wymiar jest takim samym wymiarem jak pozostałe. Nic go nie wyróżnia. Te wymiary (kierunki w kosmosie) zamieniają się ze sobą znaczeniami wyłącznie w zależności od ruchu i wyboru układu odniesienia. To co dla jednych jest przestrzenią, dla innych jest wymiarem obrazującym upływ czasu. Nie wiem jak dla Was, ale dla mnie to zaskakujące. Skrajny przypadek jest chyba taki: obserwator poruszający się jak foton względem nas z prędkością światła może powiedzieć, że siedzi sobie spokojnie na kanapie i że to my poruszamy się w jego 3D z zawrotną prędkością światła. cdn.
-
No cóż, zdania są podzielone. Spróbuję za pomocą metod statystycznych wykazać, że rezonanse to przypadek. Może się uda... Fajnie by było, gdyby ktoś zweryfikował wzór na liczbę koniunkcji, który podałem. Sprawa wydaje się prosta, ale mnie to sprawiło problem i warto zweryfikować, czy się nie pomyliłem. Napisałem też, że gdyby wartość rezonansu była liczbą niewymierną, to do spotkań mogłoby w ogóle nie dochodzić. To raczej nieprawda. Do spotkań nie dojdzie, jeżeli będzie rezonans 1:1 i dowolne przesunięcie. W innych przypadkach jedno z ciał będzie "szybsze" i dogoni to drugie. A więc pojawia się szersze pytanie: jeżeli rezonans jest liczbą niewymierną, to ile jest koniunkcji?
-
Oczywiście, że to nie mój "wynalazek". Wiesz może, czy występowanie tych rezonansów jest powszechnie uznane przez naukowców? I jakie są przyczyny, że tak się dzieje z orbitującymi ciałami? (Jeżeli nie masz gotowej odpowiedzi, to spróbuję to wyczytać z wiki.)